Are Independent Variables in Experimental Research Categorical or Continuous

An independent variable is an effect which potentially influences the outcome of an experiment. It can be an independent variable of interest, which the researcher specifically manipulates to test a predefined hypothesis, or a nuisance variable, which is of no particular interest in itself, but needs to be controlled or accounted for in the statistical analysis, so that it does not conceal the effect of a variable of interest.

Content:

• Independent variable of interest
• Nuisance variable
  • Standardising a nuisance variable
  • Randomising across a nuisance variable
  • Blocking a nuisance variable
  • Nested variables
  • Covariate
    • Checking if including a covariate is appropriate
    • Why it is important that the assumptions for covariate inclusion hold
  • Uncontrolled variable
• Continuous and categorical variables
• Allocation of experimental units into the categories of a variable
• Repeated factor
• Representing variables in the EDA
  • Representing independent variables of interest in the EDA
  • Representing nuisance variables in the EDA

Independent variable of interest

This is also known as a predictor variable or a factor of interest. It is an "input" variable and is a factor that a researcher manipulates within a controlled environment in order to test the impact that changing the levels of the independent variable has on the outcome measured. In an experiment testing the effect of a pharmacological intervention, the variable could be a drug with categories such as 'vehicle control', 'low dose' and 'high dose'. In an experiment testing the effect of a surgical intervention such as an ovariectomy, the variable would be the surgery, with categories such as 'sham ovariectomy' and 'ovariectomy'.

Often, an experiment has several variables of interest. Independent variables of interest can be included as factors of interest in an analysis. A factor (be it of interest or nuisance) is a mathematical construct created by the experimenter to allow them to quantify an effect. As such, factors can have continuous numerical levels or categorical levels, depending on the nature of the underlying effect, the reasons for including it in the experimental design and any questions the experiment aims to answer.

Back to top

Nuisance variable

Nuisance variables are other sources of variability or conditions which may influence the outcome measure. Any particular experiment is likely to have several nuisance variables which are known, or suspected, to impact on the outcome but are not of direct interest to the researcher.

There are two separate concerns with nuisance variables. The most serious one is that, by chance, they are confounded with the variable of interest. This risk is mitigated by randomisation and an appropriate sample size. The second issue is that nuisance variables may increase the variability of the responses if not accounted for, thus inflating the noise against which the researcher is trying to detect the signal of interest. Identifying these nuisance variables and accounting for them increases the sensitivity of the experiment to detect changes induced by the variable(s) of interest and can help reduce animal use.

Deciding on whether an independent variable is of interest or a nuisance variable depends on the objective of the experiment, the same variable may be a nuisance variable in one experiment, but may be a variable of interest in a different experiment. For example, age can affect behaviour, so in an experiment looking at the effect of a dopamine agonist on behaviour, if the rats to be used have a wide age range, age would be a nuisance variable which should be accounted for. If it is not accounted for the changes induced by the dopamine agonist could be concealed by the additional variability caused by age differences.

In contrast, if the objective of the experiment is to investigate the effect of the dopamine agonist in young and old animals then both drug and age are independent variables of interest and the experiment should be designed to allow both to be assessed.

When designing an experiment, a crucial step is to identify which nuisance variables are likely to affect the outcome of the experiment. The type of things to consider may include cages or rooms, if the animals are not all housed together, the day or time of the intervention or measurement, or the person doing it if animals are not all processed the same day, or by experimenters with different levels of skills. The list could be endless but the important thing is to identify what is relevant to a particular experiment, based on common sense and past experimental results, and always keep trying to identify new sources of variability.

Back to top

Standardising a nuisance variable

Standardisation involves keeping the nuisance variable constant across all experimental units.

An example of a nuisance variable can be the piece of equipment that is used for a measurement. In an experiment to test blood pressure after a drug intervention, if all control measurements are recorded on one piece of equipment, and all treatment measurements are recorded on a second piece of equipment then differences between group measurements could be due to the treatment or the calibration of the equipment used. The two variables are said to be completely confounded and there is no way of separating their effects.

One possible way to deal with this is to standardise the variable and use the same equipment for both groups, however this might not always be practical. If a measurement takes a long time to perform then restricting an experiment to one piece of measurement apparatus will increase the length of the experiment. Furthermore this could introduce a different type of variability as the measurements may instead need to be done over a period of two days, instead of one.

Standardising variables can also reduce the external validity of the experiment. For example sex of the animals used may be a nuisance variable, but while choosing to only use males in an experiment may decrease the variability of the response (depending on the response being measured), the results might not applicable to females.

Back to top

Randomising across a nuisance variable

If animals (or experimental units) are randomised into treatment groups using an appropriate method of randomisation (see allocation section), then the investigator can assume that the observed effects of the variables of interest are not unduly influenced by nuisance variables.

The purpose of randomisation is to prevent bias, either intentional or unintentional, from being introduced into the experiment by the investigator. Randomly assigning the experimental units to groups ensures that inherent and inescapable differences between experimental units are spread among all treatment groups with equal probability.

For example the location of a cage of animals within the room can be a nuisance variable; temperature may vary at different places within a room, and being housed close to the doors may increase stress levels in an experimental animal. However it is not possible to standardise this variable and keep all cages in the exact same location. Thus an alternative approach is to randomise across the nuisance variable and allocate every cage of animals at random to a location within the housing racks in the room. With a complete randomisation however, and especially with a small sample size, there is a risk that the majority of the treatment cages may end up being placed together, by chance.

Back to top

Blocking a nuisance variable

Using a nuisance variable as a blocking factor in an experiment involves breaking down the experiment into a set of mini-experiments or blocks, where each block contains a subset of the experimental units that are similar to one another. The blocking factor is the variable that is used to indicate how the experimental units were grouped into blocks.

Consider again the nuisance variable of location of animals within a housing facility. To avoid the possibility of all treatment cages randomly being placed near the door, while the control cages are placed in a quieter area away from the door, block randomisation can be used to allocate each cage to a location within the room. This would involve splitting the possible cage locations into blocks based, for example, on proximity to the door and the level of the housing rack. The control cages and the treatment cages are then assigned randomly within these blocks. This ensures that any effect due to the location of the cage within the room is split equally between all experimental groups.

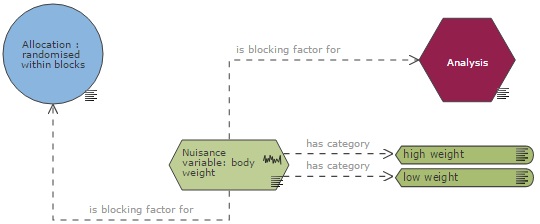
Blocking may be necessary due to practicalities in the study design, such as a need to carry out interventions over a period of 3 days, or the need to use multiple pieces of recording equipment. Animal characteristics such as age or body weight can also be used as blocking factors, to decrease the underlying between animal variability. By definition, only a categorical variable can be used as a blocking factor, as the categories identify the blocks. However, a continuous variable such as body weight can be used as a blocking factor if it is converted into a categorical variable with a set number of weight range categories, for example 'low weight', 'medium weight' and 'high weight' animals.

Examples of nuisance variables which could be considered as blocking factors if they are known or suspected to introduce variability to the results include:

• Time or day of the experiment – interventions or measurements carried out at different times of the day or on different days
• Investigator or surgeon – different level of experience in the people administering the treatments, performing the surgeries, or assessing the results may result in varying stress levels in the animals or duration of anaesthesia
• Equipment (e.g. PCR machine, spectrophotometer) – calibration may vary
• Animal characteristics – marked differences in age or weight
• Cage location – exposure to light, ventilation and disturbances may vary in cages located at different height or on different racks, which may affect important physiological processes

Including a blocking factor in the randomisation ensures that the variability induced by that nuisance variable is split between the groups, this is sometimes known as a stratified randomisation. It is important to include a blocking factor in the randomisation, where appropriate, as otherwise:

1. There is still a risk that the additional variability caused by the blocking factor will be included in the variability of the response
2. There is a risk that treatment allocation is unbalanced across the blocks will bias the treatment comparisons.

Unless the blocking factor is included in the statistical analysis, the variability of the data (assuming the blocking factor is influential) is increased by doing this. For example, consider a situation where animal bodyweight is included as a blocking factor in the randomisation of four treatments to ensure that the effect of the drug is not confounded by the animals' weight, which might influence pharmacokinetics. Animals are separated into blocks of four based on their bodyweight, and the four treatments are randomly assigned to each block so that each treatment is allocated to one of the four largest animals, one of the next four largest (etc.) and finally one of the four smallest animals. Effectively this has artificially spread the animals (within each treatment group) across the bodyweight range. If small animals do react differently to large animals, then this has artificially increased the variability of the data by making sure the bodyweight range within each treatment group are spread as far as possible-this introduces the variability due to bodyweight into the variability of the response.

Once the blocking factor has been included in the randomisation it is important that the nuisance variable is included in the analysis as a blocking factor or as a covariate to account for the additional variability discussed above. Including it in the analysis reduces the variability within the treatment group caused by the blocking factor and increases the precision of the effect of treatment, thus increasing the ability to detect a real effect with fewer experimental units. Nuisance variables can be included in the analysis as either a covariate or a blocking factor. There are a few reasons for choosing one over the other:

1. If the factor is clearly a categorical factor, then it should be a blocking factor (i.e. pieces of equipment, days of the week).
2. If the factor can be either categorical or continuous (i.e. bodyweight) then the covariate only needs 1 degree of freedom whereas the blocking factor needs b-1 degrees of freedom (where there are b blocks). This might be an important consideration in smaller designs.
3. Covariates need linear relationships between the response and the covariate whereas blocking factors don't.

The Allocation page has more information on blocking factors.

Back to top

Nested variables

A variable is nested within another variable when each category of the nested variable is found within one and only one category of the variable it is nested in. For example in an experiment involving histological sections of mouse brain, where the mouse is the experimental unit, the variable 'histological section' is nested within the experimental unit 'mouse' because each of the histological sections is associated with only one mouse. All sections from the same mouse receive only one intervention because the mouse is the experimental unit – the whole mouse is subjected to the intervention (e.g. 'running' or 'no running') independently of other mice.

It is important to identify variables which are nested at a level below that of the experimental unit, and take them into account when analysing experimental data in order to prevent pseudoreplication. This occurs when observations are not statistically independent but are treated as if they are and can lead to false positive conclusions.

Pseudoreplication due to nesting can also occur when taking multiple samples from an animal. For example, in an experiment investigating the effect of a drug on the response of individual neurons, the experimental unit is the animal even though multiple neurons are recorded from each animal. In this case the individual neurons are nested within the individual animal. The analysis should be carried out using one measurement per animal, rather than using the data from each neuron measured. To achieve this the data should be averaged for each animal before running the statistical analysis. This approach reduces the between animal variability as the multiple replicates measured per animal are used to produce a more precise single measurement. In general it is recommended to always average up to the experimental unit level, unless a specialist analysis is performed to investigates the variability associated with the multiple nested variables or the responses are measured over time and are analysed using a repeated measures approach.

Back to top

Covariate

The variability associated with a continuous nuisance variable can be accounted for by including it as a covariate in the statistical analysis. This may be done if experimental units differ due to the influence of a continuous nuisance variable that is not readily controllable. Examples of variables that can be used as covariates include a pre-treatment measure of the response of interest, baseline bodyweight or age of the animal. These values should ideally be measured before the animal undergoes any intervention that corresponds to a variable of interest.

The purpose of using a variable as a covariate is to capture background information that may influence and explain post-experimental differences between individual experimental units. For example, there may be a baseline measurement that has a strong relationship with the response of an animal to a treatment, and some of the post-intervention variability in the response can be explained by accounting for the variability in the baseline measurements.

An example of this may be when examining the effect of a novel compound on locomotor activity. The more active animals before treatment are likely to be the more active animals at the end of the study, regardless of the treatment they received. Using baseline locomotor activity as a covariate would take this into account and thus reduce the overall post-intervention between animal variability and so increase the statistical power of the test for effects of the independent variable of interest.

Back to top

Checking if including a covariate is appropriate

To decide if a covariate should be included in the statistical analysis check that it meets the assumptions below:

1. The covariate is independent of treatment.
2. There is a strong relationship between the outcome measure and the covariate. It is only worth fitting the covariate if there is a strong positive (or negative) relationship (i.e. the covariate and outcome measure increase together, decrease together, or when one increases the other decreases), otherwise it can reduce the power of the experiment.
3. The relationship between the outcome measure and the covariate is similar for all treatments.

These assumptions can be tested by plotting the data, for example using a categorised scatterplot. Plot the primary outcome measure against the covariate, colour coded by the treatment groups, as seen in the examples below. The graphs below are adapted from output automatically generated in InVivoStat when a covariate is included in the statistical analysis.

For the first assumption to hold, the covariate values should not be different across the groups in the analysis. In the graph below, data from the drug and control groups are separated along the x-axis. This indicates that the covariate is different in the drug treated group and the control group and therefore the covariate is not independent of the treatment. We do not recommend including this covariate in the analysis.

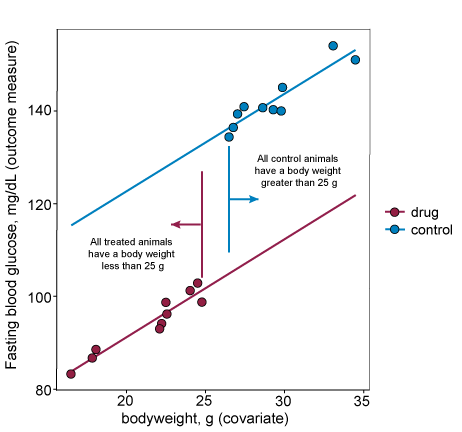
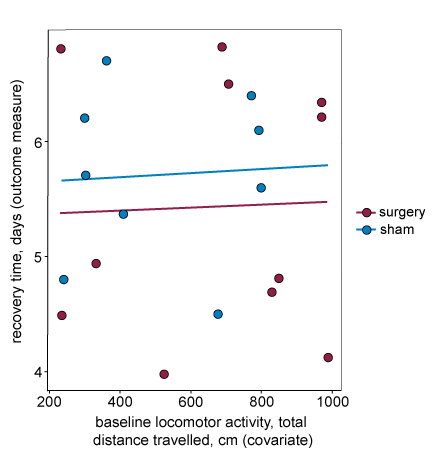
For the second assumption to hold, the covariate should explain some of the variability in the outcome measure, this happens when the outcome measure and the covariate are correlated. In the graph below, the lines on the plot are almost horizontal, indicating that there is a weak relationship between the covariate and the outcome measure. If the covariate is included in the statistical analysis then it will not explain enough of the variability in the outcome measure to justify its inclusion, and could reduce the power of the experiment. We do not recommend including this covariate in the analysis.

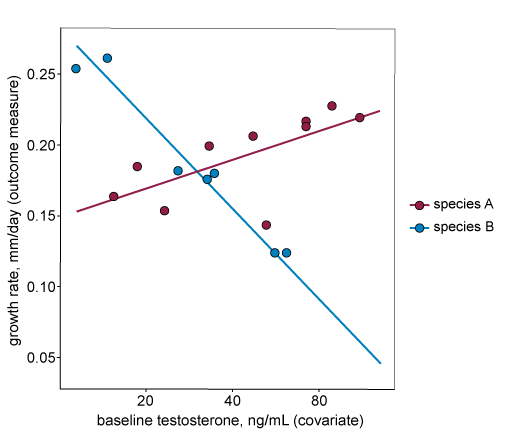
For the third assumption to hold, the covariate should have the same effect in all treatment groups (i.e. the relationship between the outcome measure and the covariate is the same for all treatment groups). In the graph below, the lines (each representing a separate treatment group, in this case a different species) are not parallel. This indicates that the relationship between the outcome measure and the covariate is different for each treatment group. We do not recommend including this covariate in the analysis.

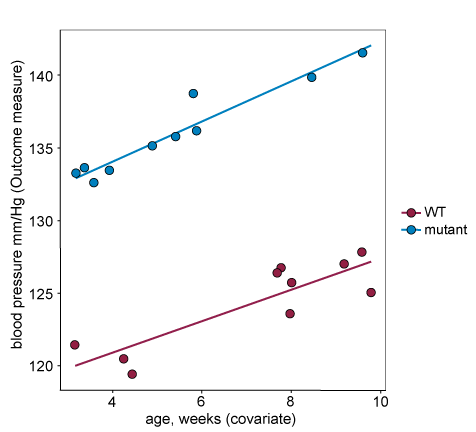
In the example below all three assumptions hold:

1. There is no treatment effect of the covariate (there is a horizontal overlap between the two treatment groups along the x-axis).
2. The response and covariates are positively correlated, so the covariate does explain the between animal variability in the response and hence is worth including in the statistical analysis (i.e. including it will not reduce power).
3. The lines on the plot are parallel, indicating that the response/covariate relationships are similar across the two treatment groups.

In many cases you will not know if including a particular covariate in the analysis is appropriate when planning an experiment. In these cases, measure the covariate during the study, but only include it in the statistical analysis if the assumptions for covariate inclusion are met.

Back to top

Why it is important that the assumptions for covariate inclusion hold

When including a covariate in a statistical analysis, such as ANCOVA, group means used in the analysis are adjusted to correspond to the predicted level of the outcome measure at the overall average of the covariate. A mean adjusted in this way (i.e. what the group mean would be at the overall average of the covariate) is often called the predicted mean. Groups are then compared using the predicted mean for each group at the overall average of the covariate, see graph below. For this approach to generate reliable predicted means, and reliable comparisons between the means, the assumptions described in the section above must hold.

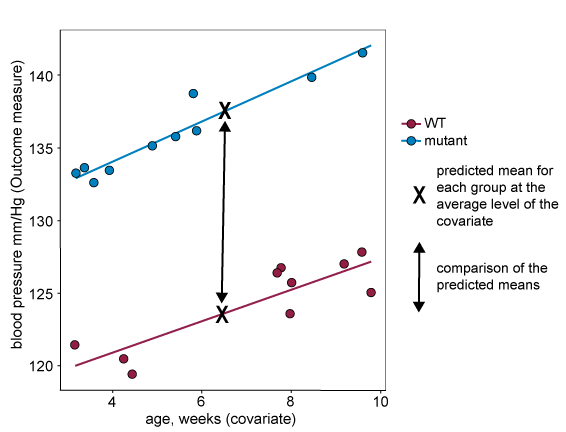
If the covariate levels are systematically different across the treatment groups, then the predicted mean at the overall average level of the of the covariate can be misleading and not reflect the actual data. In the example below (where assumption 1 does not hold), the predicted mean for the treatment group 'drug' is higher than all actual responses from that group.

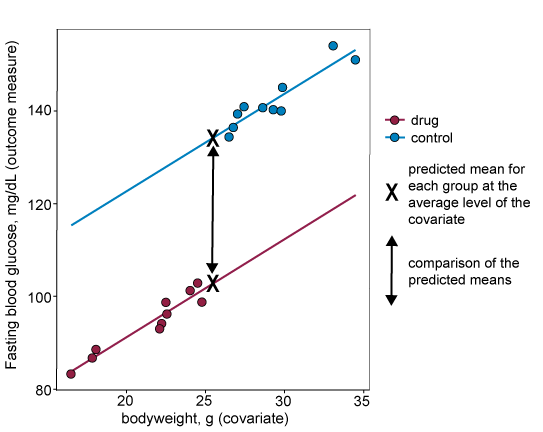
If the lines are not parallel (i.e. if assumption 3 does not hold), then the size of the difference between predicted means will depend on the level of the covariate where the comparison is made. On the graph below, the difference between predicted means in the analysis (marked with an X on the graph) will be very small despite the fact that there is evidence of the intervention having a large effect at more extreme levels of the covariate.

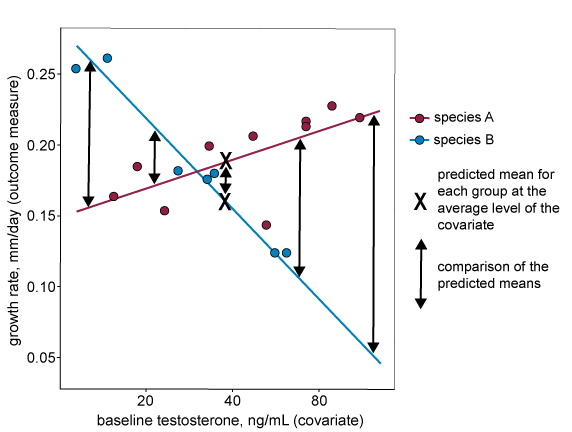
If the lines are parallel then the size of the difference between predicted means is independent of where along the covariate the comparison is made (i.e. the size of the difference is the same regardless of covariate level), see graph below. This means that the difference between predicted means is a reliable estimate of the treatment effect.

Back to top

Uncontrolled variable

In some instances it is not possible to control for a nuisance variable.

For example, in an experiment comparing measurements from wild type and mutant litters when only a limited number of animals can be obtained at any one time, then the day of measurement would be a nuisance variable and ideally used as a blocking factor to ensure an equal number of measurements from mutant and wild type animals are made on each day. However if the litters are born at different times and animals from the two genotypes cannot be recorded on the same day then the day of the experiment cannot be used as a blocking factor. In this case it is not possible to avoid confounding the nuisance variables 'day' with the variable of interest 'genotype' and the day variable remains uncontrolled.

The only protection against such nuisance variables is adequate replication so that the randomization strategy makes it unlikely that the nuisance variable is confounded with the independent variable of interest (genotype in the example above). If adequate replication is not possible, such that a confound remains, then the experiment may not be worth carrying out.

Back to top

Continuous and categorical variables

Variables can be categorical or continuous:

Continuous variables include truly continuous variables but also discrete variables. Levels consist of numerical values, for example bodyweight, age, time to event.

Categorical variables have levels that are non-numeric, for example sex (categories: 'male' and 'female'). Categorical variables can be ordinal, nominal or binary.

Some variables can be considered as either, for example drug dose (levels: 'vehicle', 'low' and 'high' dose, if it is categorical, or levels: 0, 1 and 10, if it is continuous) or time can be considered continuous or distinct time points (levels: 'pre-intervention' and 'post-intervention').

Deciding to treat a variable as continuous or as categorical depends on the objective of the experiment. For example treating drug dose as a continuous variable enables modelling of the dose-effect relationship, perhaps with a curve or regression line, and the underlying relationship between dose and effect can be estimated. The analysis provides an estimate of the relationship – it will not test a hypothesis but identify the dose that causes a biologically relevant effect (which might not be one of the doses assessed).

Treating drug dose as a categorical factor enables a comparison between the individual treatment group means and a test of the null hypothesis (H₀) that there is no difference between the groups treated with vehicle, low and high doses.

This choice impacts on the experimental design. If drug dose is treated as categorical the experimental design should include a limited number of dose groups but each group should contain sufficient animals to power the pairwise tests. If drug dose is treated as continuous it would be best to include more doses in the design, with fewer animals at each dose.

For nuisance variables treating a variable as continuous or categorical depends on how the variability is accounted for. Categorical variables can be used as blocking factors, and continuous variables can be used as covariates. If a nuisance variable can be considered as either, it can be used differently in the allocation and the analysis, for example body weight can be considered categorical and used as a blocking factor in the allocation (categories: 'low weight' and 'high weight') and as a continuous covariate in the analysis.

Back to top

Allocation of experimental units into the categories of a variable

Experimental units are allocated to the different categories (or levels) of a particular variable, to test the effect of a variable of interest or to control the effect of a nuisance variable. This allocation should be random (see randomisation section) and in most cases, it will be possible to randomise experimental units to a variable's categories.

For some variables, for example animal characteristics such as sex or genotype, even though the randomisation is not done by the experimenter, it can be assumed that animals have been allocated into the male or female categories, or to a particular genotype, at random, via Mendelian inheritance.

However, for other variables, it is not possible to allocate experimental units at random. For example in an experiment where body weight is used as a blocking factor, animals cannot be randomised into weight ranges; they are allocated to the different categories of that nuisance variable based on their body weight. It is important to realize that for such variables, because allocation has not been random, it is impossible to conclude that any relationship is causal (e.g. that body mass, rather than something correlated with body mass, causes the difference in response) but it nonetheless may be a useful predictor of the response.

Back to top

Repeated factor

In a situation where animals (or experimental units) are repeatedly measured over time, and time is a variable of interest, then 'time' is a repeated factor. Note the levels of a repeated factor cannot be randomised, 'day 1' must come before 'day 2'.

A repeated factor is a variable of interest which is shared across all animals in the experiment and it is not randomised (also known as within subject factor). There are two situations where including a repeated factor of interest would be appropriate: in repeated measure designs anddose escalation designs.

In a repeated measure design, the measurements for each animal or experimental unit are obtained in a non-random order, for example the animals are measured at specific time points or in specific brain regions which cannot be randomised (t₀ always comes before t₁, brain is scanned front to back). The repeated factor would then be 'timing of measurement' or 'brain region' and all animals are measured across all categories of these variables.

In a dose-escalation design, animals receive multiple treatments (and measurements) over time in a non-random order, for example escalating doses of a drug to avoid toxicological effects. The variables 'drug' and 'timing of measurement' are combined together because all animals get the same dose at the same time. The repeated factor would then be 'drug' and all animals are measured across all categories (drug doses).

The crucial difference between arepeated measure anddose escalation design is that in a repeated measure design the experimental unit is usually the animal (which is then measured repeatedly), whereas in the dose-escalation design it is the animal within a time period that is the experimental unit and so each experimental unit is measured only once.

If the order of the repeated measurements can be randomised, it would not be appropriate to include the variable which relates to the timing of measurement or the test period as a repeated factor in the analysis. In a crossover design for example, where each animal receives multiple treatments in a random order and each animal is used as its own control, 'timing of measurement' would be a blocking factor for the analysis.

Back to top

Representing variables in the EDA

In the EDA diagram, different nodes are used for independent variables of interest and nuisance variables. Variables can be categorical or continuous; this can be indicated in the properties of the variable node. If a variable is categorical, categories nodes defining the levels of the factor should be linked to the variable node. In the properties of the independent variable nodes, the field 'categorical or continuous' relates to how the variable is treated in the analysis.

For the variables of interest, variable categories nodes are used as 'tags' on the diagram. Variable categories can be tagged to three different types of nodes:

• Intervention nodes – for example when the independent variable is treatment such as the variable of interest 'Drug A' in Example 1, which has two categories: 'vehicle' and 'drug', these variable categories are used to tag the two intervention nodes to indicate the treatment each group of mice receives.
• Group nodes – for example when the independent variable is an animal characteristic such as 'sex' in Example 3. The two categories 'male' and 'female' are tagged to the groups to indicate the composition of each experimental group.
• Measurement nodes – for example when the independent variable relates to a timing such as 'time of measurement' in Example 3. Then each time point is represented as a category node and tagged to the relevant measurement nodes.

For clarity, several instances of the same variable categories can be included on the diagram. In Example 1, the two categories nodes have been duplicated to prevent arrows running across the diagram. The system will considers nodes with the same labels, several instances of the same category

Similarly, several instances of the same variable can be included on the diagram, in Example 2, the nuisance variables 'test period' and 'animal' each appear twice on the diagram. The nodes have been copied and pasted to prevent arrows running across the diagram. Only one instance of each variable has to be defined; if multiple nodes exist for the same variable, the variable should be defined with the node that is connected to the analysis, categories should be connected to this node and relevant information should be provided in its properties. This is to enable the system to provide recommendations regarding the method of statistical analysis.

Variables can be categorical or continuous; this needs be indicated in the properties of the variable node so that the system can recommend an adequate analysis recommendation.

Experimental units are allocated to the different categories of variables. In the EDA diagram, for all variables of interest and nuisance variables, how the experimental units are allocated to categories can be indicated in the properties of the variable nodes.

Back to top

Representing independent variables of interest in the EDA​

In the EDA diagram, to indicate that an independent variable of interest is a factor of interest in an analysis, the nodes are connected as shown in the picture below.

Often, an experiment has several variables of interest, each should have its own independent variable of interest node, as demonstrated below.

In the example above, in an experiment looking at the effect of exercise on neuronal density, there are two variables of interest:

• exercise with two categories: 'running' and 'no running', animals are randomised by the investigator into one of these two categories to test the effect of exercise on neuronal density
• sex with two categories: male or female, to check whether the effect of exercise differs between males and females

It is also important to identify repeated factors correctly in an EDA diagram as this has implications for the analysis. Whether a variable of interest is a repeated factor can be indicated in the properties of the variable node.

Back to top

Representing nuisance variables in the EDA

Nuisance variables are other sources of variability or conditions which may influence the outcome measure and are indicated on the EDA diagram using nuisance variable nodes.Depending on the type of nuisance variable and the objective of the experiment, there are different options to account for the variability; the variable could be standardised, randomised across, blocked, nested within another variable or used as a covariate. If none of these things are done, then the variable is deemed uncontrolled. This information should be provided in the properties of the nuisance variable nodes.

In the EDA diagram, standardised nuisance variables are indicated with only one category. They are not connected to the rest of the diagram because once standardised they do not add variability to the experiment. Standardising nuisance variables will limit how far the conclusions of the experiment can be generalised.

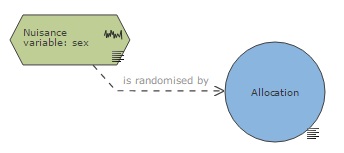
In the EDA diagram, to indicate that a nuisance variable is accounted for by randomisation, it should be connected to the allocation node with a link 'is_randomised_by'.

In the EDA diagram, to indicate that a nuisance variable is a blocking factor, it should be connected to both the allocation and the analysis nodes, with a link 'is_blocking_factor_for'. For more information on randomisation with blocking factors go to the allocation section.

In the EDA diagram, a nested nuisance variable is indicated by connecting it to the variable it is nested within. Nested variables can be linked to any other variable and also the experimental unit node.

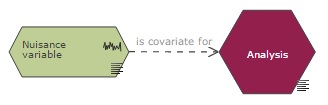
In the EDA diagram, a nuisance variable used as a covariate is indicated by connecting it to the analysis node with the link 'is_covariate_for'.

Anyuncontrolled nuisance variablesshould be flagged as uncontrolled in the EDA diagram and should be connected with a link to the measurement and the analysis nodes using the link 'causes_variation_to'.

Back to top​

References and further reading

BATE, S. T. & CLARK, R. A. 2014. The Design and Statistical Analysis of Animal Experiments, Cambridge University Press.

DAYTON, C. M. 2005. Nuisance Variables. In: EVERITT, B. & HOWELL, D. (eds.) Encyclopedia of Statistics in Behavioral Science. John Wiley & Sons, Ltd.

DEAN, A. M. & VOSS, D. 1999. Design and Analysis of Experiments, Spring-Verlag.

FESTING, M. F. W., OVEREND, P., GAINES DAS, R., CORTINA BORJA, M. & BERDOY, M. 2002. The design of animal experiments: reducing the use of animals in research through better experimental design, London UK, Royal Society of Medicine.

GAINES DAS, R. E. 2002. Role of ancillary variables in the design, analysis, and interpretation of animal experiments. ILAR J, 43, 214-22. doi: 10.1093/ilar.43.4.214

KIRK, R. E. 2009. Experimental Design. In: ROGER E. MILLSAP, A. M.-O. (ed.) The SAGE Handbook of Qualitative Methods in Psychology. SAGE Publications Ltd.

LAZIC, S. E. 2010. The problem of pseudoreplication in neuroscientific studies: is it affecting your analysis? BMC Neurosci, 11, 5. doi: 10.1186/1471-2202-11-5

campbellmosely1979.blogspot.com

Source: https://eda.nc3rs.org.uk/experimental-design-variables

Share this post